PhD selection

In this blogpost I will try to experiment how to simulate the conditions for ending a PhD program and obtaining the doctorate, from the school.

I will base this simulation on three principles:

1. There are some variables that are normally distributed.
2. There are some variables that are uniform distributed.
3. There are some variables that are not randomly distributed.

Those that are normally distributed will be simulated using the rbeta function, but I will create a symmetric distribution. Assuming that the maximum of the variables will be either 1 or -1, and the average will be 0.

library("tidyverse")
## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.0 ──
## ✓ ggplot2 3.3.2     ✓ purrr   0.3.4
## ✓ tibble  3.0.4     ✓ dplyr   1.0.2
## ✓ tidyr   1.1.2     ✓ stringr 1.4.0
## ✓ readr   1.4.0     ✓ forcats 0.5.0
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag()    masks stats::lag()
students <- 1000
inteligence <- rbeta(students, 5, 5)
sex <- sample(c("F","M"), students, replace = TRUE)
simulation <- data.frame(student = 1:students,
           inteligence = inteligence,
           sex = sex) %>% 
  mutate(grades = inteligence + runif(students))

scale01 <- function(x) {
  m <- max(abs(x))
  mm <- mean(x, na.rm = TRUE)
  (x - mm)/m
}
simulation$grades <- scale01(simulation$grades)
simulation %>% 
  ggplot() +
  geom_point(aes(inteligence, grades, col = sex))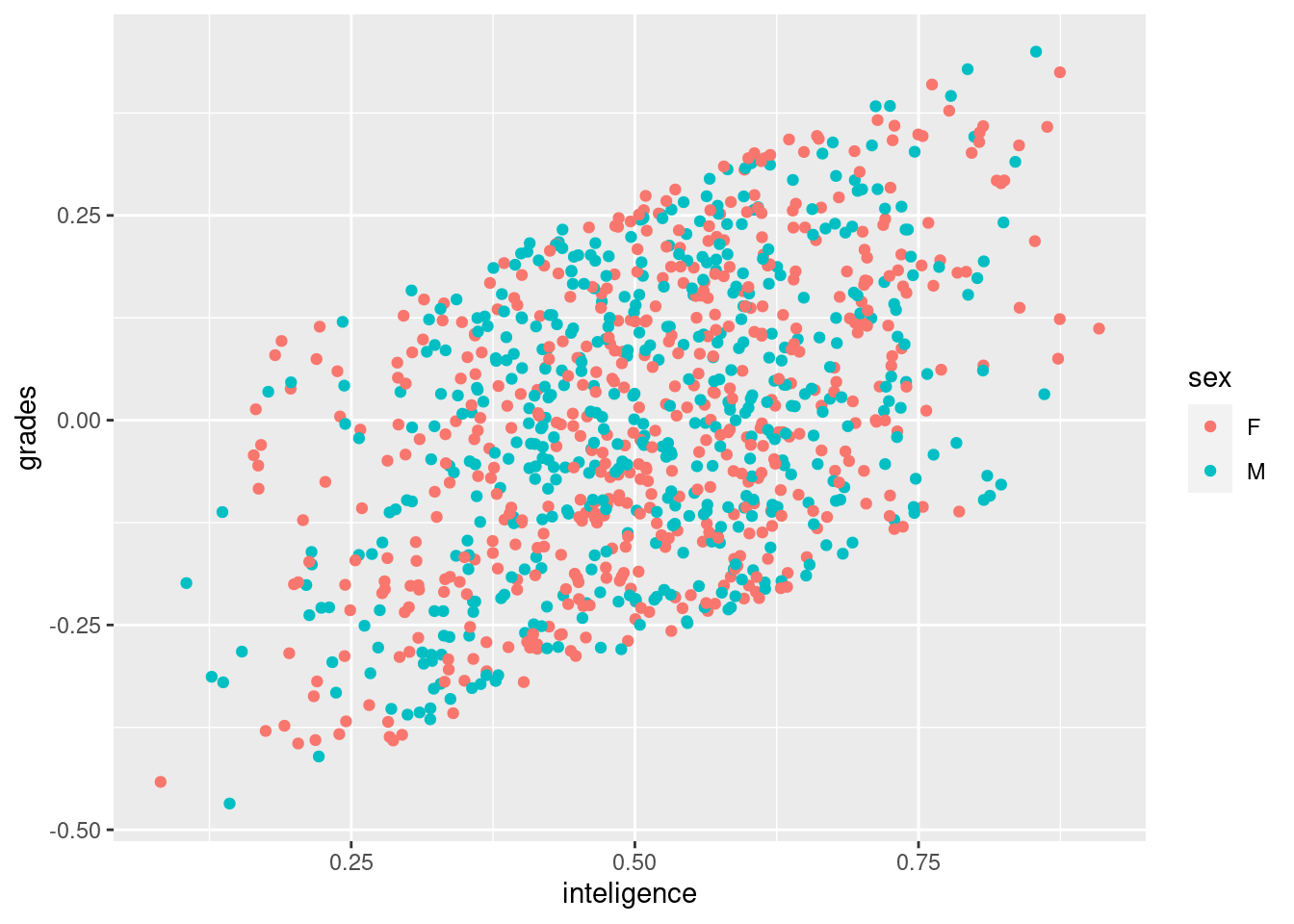

Now we suppose that the grades are based on the intelligence

simulation %>% 
  ggplot() +
  geom_histogram(aes(inteligence, fill = sex), bins = 100) +
  facet_wrap(~sex)

simulation %>% 
  ggplot() +
  geom_histogram(aes(grades, fill = sex), bins = 100) +
  facet_wrap(~sex)

Now we can simulate some other variables